Công Thức Tính Diện Tích Hình Thang và Ứng Dụng Thực Tiễn

Công Thức Tính Diện Tích Hình Thang là kiến thức toán học cơ bản, được ứng dụng rộng rãi từ học tập đến đời sống. Nắm vững công thức này là điều cần thiết để giải quyết các bài toán phức tạp hơn. Bài viết dưới đây của Xe Tải Sơn Tùng sẽ cung cấp công thức tính diện tích hình thang, hướng dẫn áp dụng và một số bài toán ví dụ.

Hình Thang là gì?

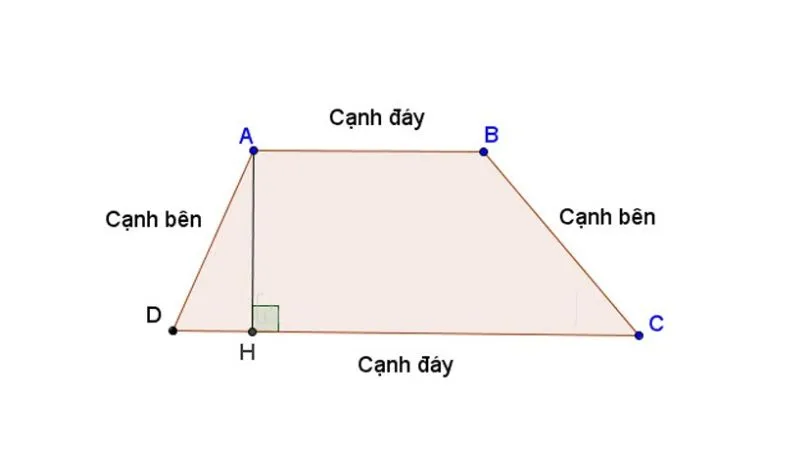
Hình thang là hình tứ giác lồi thường gặp trong toán học và thực tiễn. Hình thang có hai cạnh đáy song song với nhau và hai cạnh còn lại được gọi là cạnh bên. Diện tích hình thang được hiểu là diện tích của mặt phẳng nằm bên trong 4 cạnh tạo nên hình thang. Có nhiều loại hình thang như hình thang vuông, thang cân, hình chữ nhật, hình bình hành…

Cụ thể là:

Hình thang vuông: Hình thang có chứa một góc vuông (90 độ).
Hình thang cân: Hình thang có hai góc kề cạnh đáy bằng nhau, 2 cạnh bên có chiều dài bằng nhau nhưng không song song nhau.
Hình bình hành: Hình thang có 2 cạnh bên bằng nhau, 2 cạnh đáy bằng nhau và song song với nhau.
Hình chữ nhật: Hình thang vừa có 4 góc vuông vừa cân.

Công Thức Tính Diện Tích Hình Thang

Để tính diện tích hình thang, bạn lấy chiều dài 2 cạnh đáy cộng lại với nhau, sau đó tất cả nhân cho chiều cao rồi chia cho 2. Khi tính diện tích, bạn cần đảm bảo tất cả các số đều chung một đơn vị đo (chiều dài cạnh đáy 1 là cm thì chiều dài cạnh đáy thứ 2 cũng là cm).

Ngoài ra, trong từng trường hợp riêng biệt, bạn có thể áp dụng công thức tính diện tích hình thang như sau:

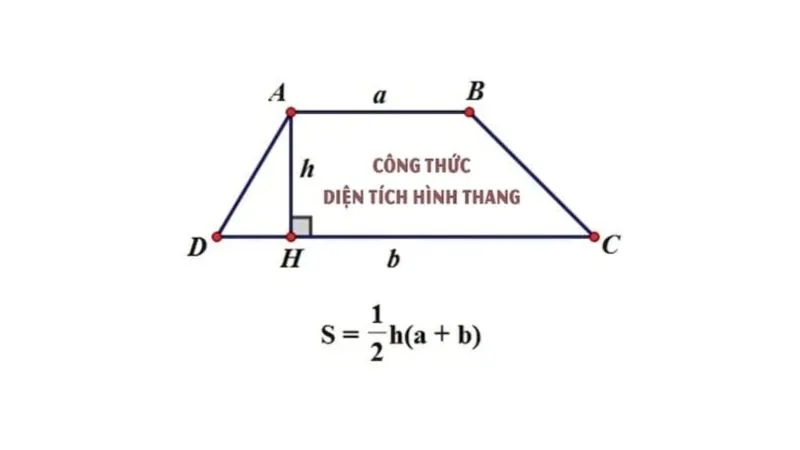
Công Thức Chung

S = h x ((a + b)/2)

Trong đó:

Diện tích hình thang: S
Chiều cao – đường nối từ đỉnh đến cạnh đáy và vuông góc với cạnh đáy của hình thang: h
Chiều dài 2 cạnh đáy: a, b.

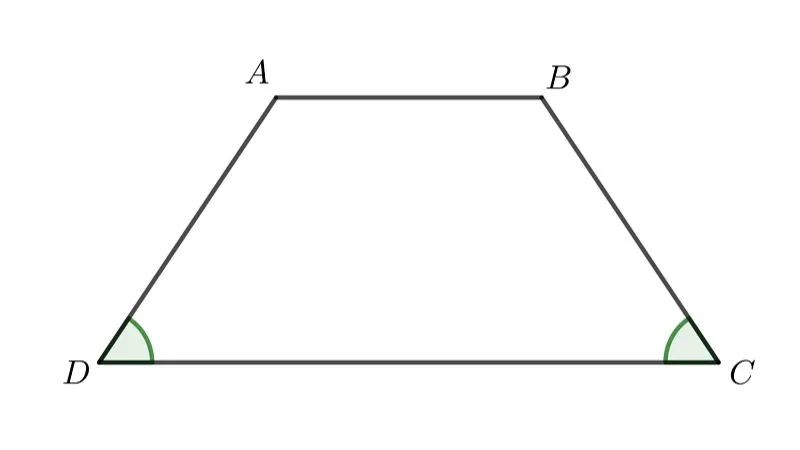
Công Thức Tính Hình Thang Cân

Hình thang cân có hai góc kề của một đáy bằng với nhau, 2 cạnh bên có chiều dài bằng nhau nhưng không song song nhau.

Nhìn chung, công thức tính diện tích hình thang cân cũng tương tự với công thức chung. Bạn cũng có thể áp dụng cách chia nhỏ hình thang thành nhiều phần để tính diện tích, sau đó cộng hết lại với nhau.

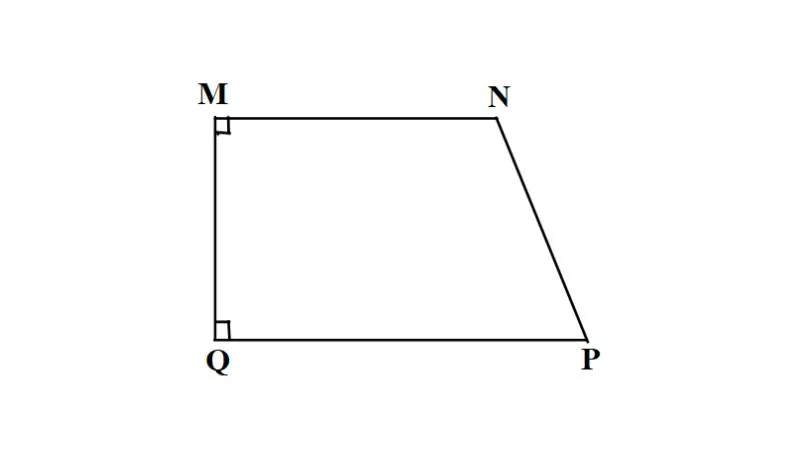
Công Thức Tính Hình Thang Vuông

Hình thang vuông chứa 2 góc vuông và một trong 2 cạnh bên vuông góc với 2 đáy.

Như vậy, công thức của diện tích hình thang vuông sẽ là: Lấy trung bình cộng của chiều dài 2 cạnh đáy nhân cho chiều cao h (h ở đây được hiểu là cạnh bên vuông góc với cả 2 đáy của hình thang). Công thức cụ thể là:

S = 1/2 h (a + b).

Hướng Dẫn Áp Dụng Công Thức Tính Diện Tích Hình Thang

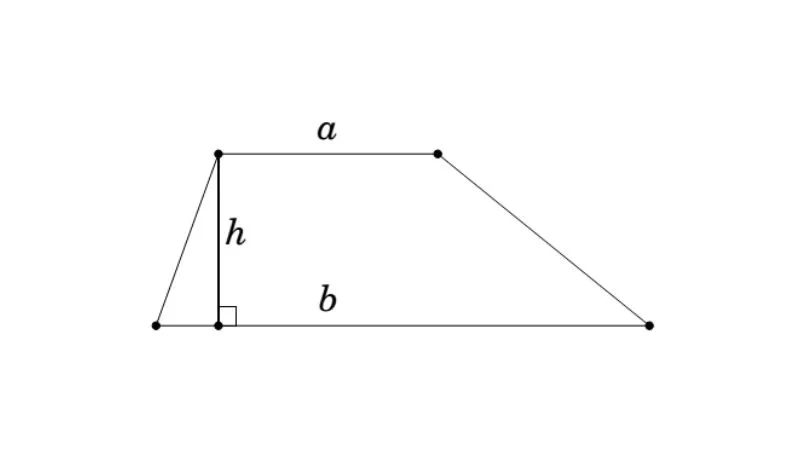
Trường hợp biết a, b và h

Trong đó, a là chiều dài cạnh đáy 1, b là chiều dài cạnh đáy 2, còn h là chiều cao nối từ đỉnh đến cạnh đáy và vuông góc với cạnh đáy của hình thang.

Bước 1: Tính tổng chiều dài của 2 cạnh đáy hình thang (a + b).

Bước 2: Xác định chiều cao h.

Bước 3: Lấy tổng chiều dài 2 đáy (a + b) nhân với chiều cao (h).

Bước 4: Lấy kết quả chia 2 (hoặc nhân với ½) để tính diện tích hình thang.

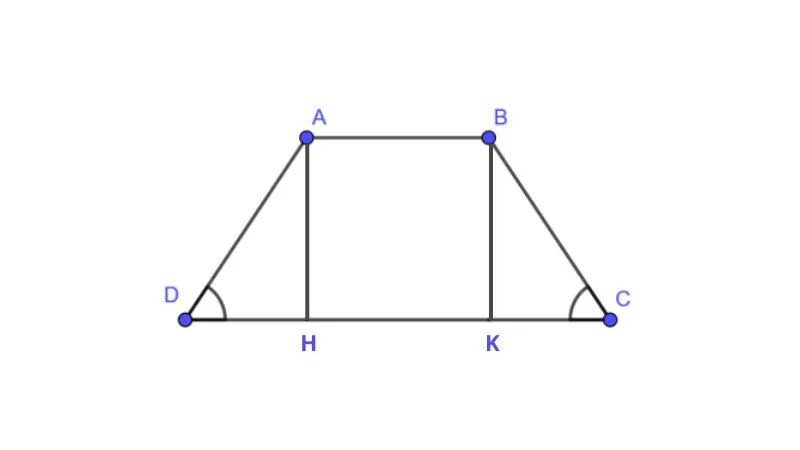
Trường hợp biết 4 cạnh (Áp dụng cho hình thang cân)

Bước 1: Chia hình thang thành các hình nhỏ hơn (2 tam giác vuông, 1 hình chữ nhật).

Bước 2: Tìm chiều dài cạnh đáy tam giác bằng cách lấy chiều dài của cạnh đáy trên trừ cho chiều dài của cạnh đáy dưới trong hình thang, sau đó chia 2.

Bước 3: Sử dụng công thức tính tam giác vuông để tìm chiều cao cho hình thang (định lý Pytago).

Bước 4: Tính diện tích hình thang với các thông số đã có.

Bài Tập Áp Dụng

Bài 1: Cho chiều dài 2 cạnh đáy và chiều cao lần lượt là 10cm, 12 cm và 7 cm, tính diện tích hình thang đó?

Bài 2: Một miếng đất hình thang có đáy lớn, đáy bé lần lượt là 20m và 24m. Sau này, người ta đã mở rộng 2 đáy lớn, đáy bé của mảnh đất với số liệu lần lượt là 3m và 5m, diện tích lúc bấy giờ đã tăng thêm 38m2 so với ban đầu. Hỏi, diện tích ban đầu của mảnh đất là bao nhiêu m2?

Kết Luận

Bài viết đã cung cấp công thức tính diện tích hình thang, hình thang vuông và một số bài tập tham khảo. Để giải đúng và nhanh, học sinh cần nắm rõ công thức và áp dụng một cách phù hợp trong những trường hợp cụ thể. Hy vọng bài viết này hữu ích cho bạn.