Công Thức Tính Chu Vi Hình Tam Giác

Chu vi hình tam giác là kiến thức toán học cơ bản được học từ lớp 2. Cách tính chu vi hình tam giác phụ thuộc vào từng loại tam giác, bao gồm tam giác thường, tam giác vuông, tam giác đều và tam giác cân. Việc tính chu vi hình tam giác đơn giản hơn so với tính diện tích hình tam giác. Bài viết dưới đây của Xe Tải Sơn Tùng sẽ hướng dẫn bạn cách tính chu vi các loại hình tam giác.

Chu vi hình tam giác

Xe Tải Sơn Tùng chuyên cung cấp dịch vụ vận chuyển hàng hóa uy tín, chất lượng. Liên hệ ngay Xe tải thuận thành Đà Nẵng Hotline : 0703233323 tới Ngay để được tư vấn và báo giá.

1. Chu Vi Tam Giác Thường

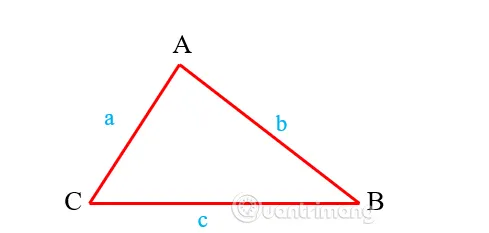
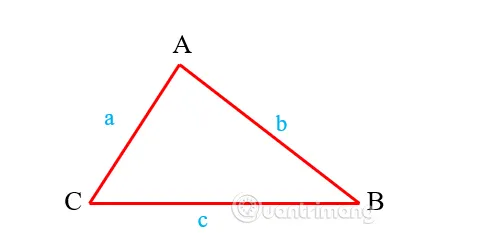
Tam giác thường là tam giác có 3 cạnh với độ dài khác nhau. Công thức tính chu vi tam giác thường như sau:

P = a + b + c

Trong đó:

• P: Chu vi tam giác.
• a, b, c: Độ dài 3 cạnh của tam giác.

Để tính nửa chu vi tam giác, ta dùng công thức: ½P = (a + b + c) / 2

Ví dụ: Một tam giác có độ dài 3 cạnh lần lượt là 4cm, 8cm và 9cm. Tính chu vi hình tam giác.

Áp dụng công thức, ta có: P = 4 + 8 + 9 = 21cm.

2. Chu Vi Tam Giác Cân

Tam giác cân là tam giác có 2 cạnh bằng nhau và 2 góc bằng nhau. Đỉnh của tam giác cân là giao điểm của 2 cạnh bên.

Để tính chu vi tam giác cân, bạn cần biết độ dài cạnh đáy và độ dài một cạnh bên. Công thức tính chu vi tam giác cân là:

P = 2a + c

Trong đó:

• a: Độ dài cạnh bên của tam giác cân.
• c: Độ dài cạnh đáy của tam giác.

Công thức này cũng áp dụng để tính chu vi tam giác vuông cân.

Ví dụ: Cho tam giác ABC cân tại A với AB = 7cm, BC = 5cm. Tính chu vi tam giác cân.

Áp dụng công thức, ta có: P = 7 + 7 + 5 = 19cm.

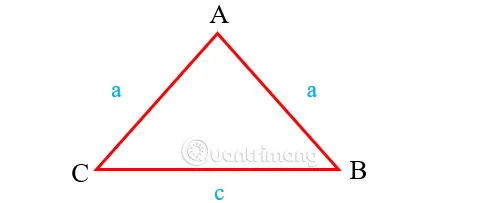Tính chu vi tam giác cân

Bạn đang tìm kiếm dịch vụ chuyển văn phòng trọn gói? Chuyển văn phòng giá rẻ Đà Nẵng, Gọi: 0965.091.910 là lựa chọn hoàn hảo cho bạn.

3. Chu Vi Tam Giác Đều

Tam giác đều là trường hợp đặc biệt của tam giác cân khi cả 3 cạnh đều bằng nhau. Công thức tính chu vi tam giác đều là:

P = 3 x a

Trong đó:

• P: Chu vi tam giác đều.
• a: Độ dài cạnh của tam giác.

Ví dụ: Tính chu vi tam giác đều có cạnh AB = 5cm.

Áp dụng công thức, ta có: P = 5 x 3 = 15cm.

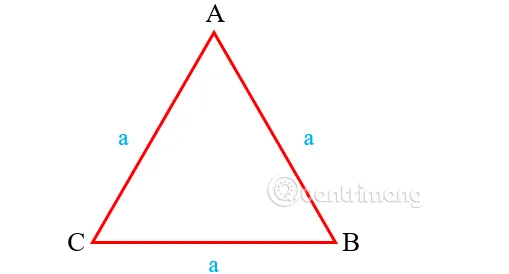Tam giác đều

4. Chu Vi Tam Giác Vuông

Tam giác vuông là tam giác có 1 góc vuông (90°). Công thức tính chu vi tam giác vuông là:

P = a + b + c

Trong đó:

• a và b: Độ dài hai cạnh góc vuông.
• c: Độ dài cạnh huyền.

Ví dụ 1: Tính chu vi tam giác vuông với CA = 6cm, CB = 7cm và AB = 10cm.

Áp dụng công thức, ta có: P = 6 + 7 + 10 = 23cm.

Ví dụ 2: Cho tam giác vuông với CA = 5cm, CB = 8cm, tính chu vi.

Vì tam giác vuông tại C, nên cạnh huyền là AB. Sử dụng định lý Pitago:

AB² = CA² + CB²

AB² = 25 + 64

AB ≈ 9,4cm

Vậy chu vi tam giác vuông CAB là: P = 5 + 8 + 9,4 = 22,4cm.

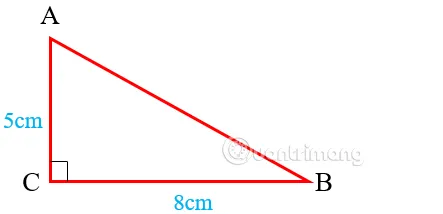Chu vi tam gác vuông

Cần thuê xe tải giá rẻ tại Đà Nẵng? Xe tải Đà Nẵng chở hàng nhanh chóng giá rẻ chỉ từ 100.000đ – Xe Tải Sơn Tùng luôn sẵn sàng phục vụ bạn.

5. Chu Vi Tam Giác Trong Không Gian

Bài toán: Trong không gian Oxy, có hai điểm A(1;3), B(4;2).

1. Tìm tọa độ điểm D trên trục Ox sao cho DA = DB;
2. Tính chu vi tam giác OAB?

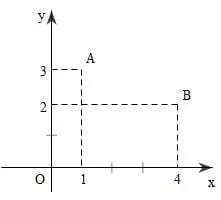Chu vi tam giác trong không gian

Lời giải:

a. Vì D nằm trên trục Ox nên tọa độ của D là (x;0).

Ta có: DA² = (1-x)² + 3²

DB² = (4-x)² + 2²

DA = DB => DA² = DB²

=> (1-x)² + 9 = (4-x)² + 4

=> 6x = 10

=> x = 5/3 => D(5/3;0)

b. OA² = 1² + 3² = 10 => OA = √10

OB² = 4² + 2² = 20 => OB = √20

AB² = (4-1)² + (2-3)² = 10 => AB = √10

Chu vi tam giác OAB: √10 + √10 + √20 = (2 + √2)√10.

Kết luận

Bài viết đã cung cấp công thức tính chu vi của các loại hình tam giác, từ tam giác thường, tam giác cân, tam giác đều, tam giác vuông cho đến tam giác trong không gian. Hy vọng những kiến thức này sẽ hữu ích cho bạn. tả một người mà em yêu quý nhất