Tin Tức
Thể Tích Khối Trụ Tròn Xoay: Công Thức và Bài Tập Vận Dụng
Thể tích khối trụ tròn xoay là một khái niệm quan trọng trong hình học không gian. Bài viết này của Xe Tải Sơn Tùng sẽ cung cấp cho bạn cái nhìn tổng quan về khối trụ tròn xoay, công thức tính thể tích, các dạng bài tập từ cơ bản đến nâng cao, cùng lời giải chi tiết giúp bạn nắm vững kiến thức này.
luyện tập phân tích và tổng hợp
1. Khối Trụ Tròn Xoay là gì?
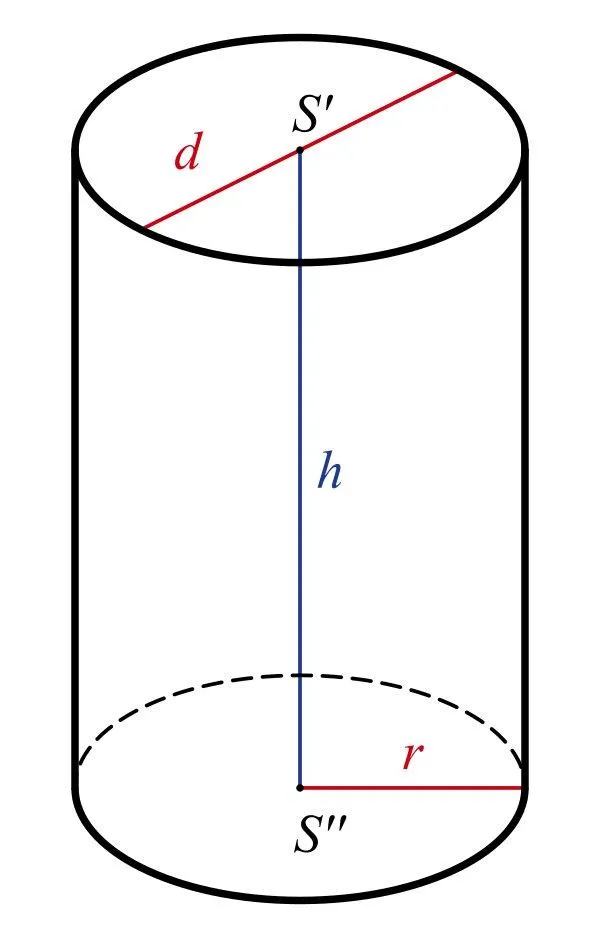
Khối trụ tròn xoay được tạo thành khi quay một hình chữ nhật quanh một trục cố định là đường trung bình của hình chữ nhật đó. Nói cách khác, khi ta quay một hình phẳng quanh một trục cố định, ta sẽ được một khối hình gọi là khối tròn xoay. Khối trụ chính là hình trụ và phần không gian bên trong nó. Thể tích khối trụ tròn xoay là lượng không gian mà hình trụ chiếm giữ.
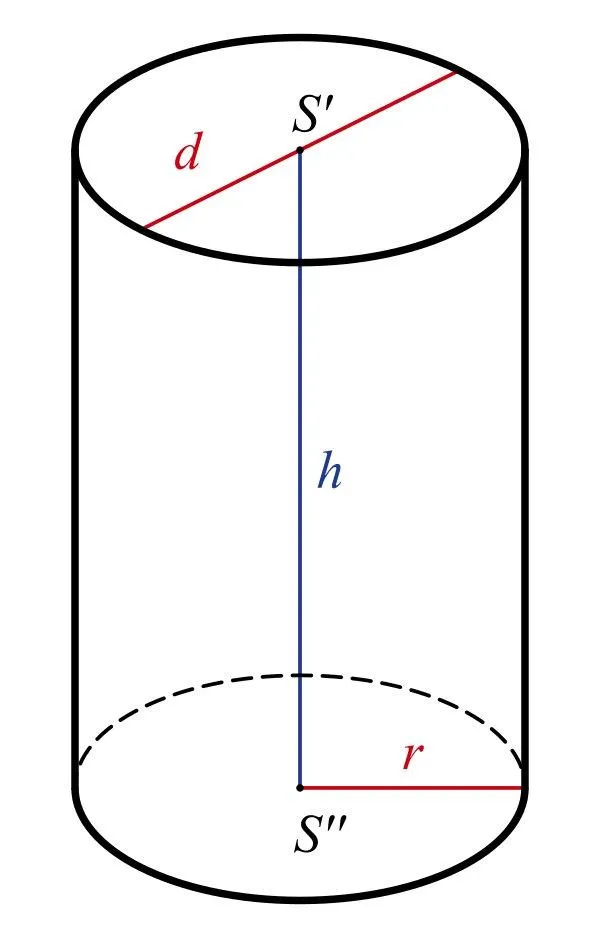Giới thiệu khối trụ tròn xoay và thể tích khối trụ tròn xoay
2. Công Thức Tính Thể Tích Khối Trụ Tròn Xoay
Để tính thể tích khối trụ tròn xoay (hay còn gọi là hình trụ), ta sử dụng công thức sau:
Trong đó:
- V là thể tích của khối trụ (đơn vị: m³)
- r là bán kính mặt đáy khối trụ
- h là chiều cao khối trụ (khoảng cách giữa hai đáy)
- π (pi) là hằng số xấp xỉ 3.14159
Công thức này thể hiện rằng thể tích khối trụ tròn xoay bằng tích của diện tích mặt đáy và chiều cao. Điều này tương tự với công thức tính thể tích khối lăng trụ.
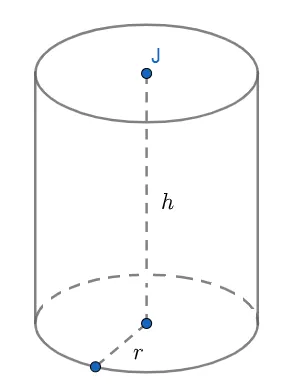Công thức tính thể tích khối trụ tròn xoay
phân tích khổ 1 mùa xuân nho nhỏ
3. Các Dạng Bài Tập về Thể Tích Khối Trụ Tròn Xoay
Dựa vào công thức tính thể tích, ta có ba dạng bài tập chính:
3.1. Tìm Bán Kính Đáy
Nếu đề bài cho đường kính, ta chia 2 để được bán kính. Nếu đề bài cho chu vi mặt đáy, ta lấy chu vi chia cho 2π.
Ví dụ: Khối trụ có thể tích πa³, chiều cao 2a. Tính bán kính đáy r.
Lời giải:
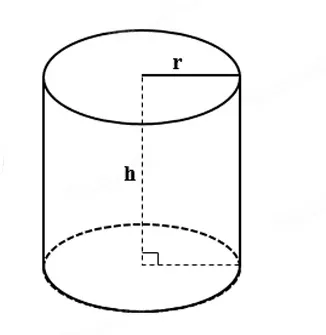Bài tập tính thể tích của khối trụ tròn xoay
Từ công thức V = πr²h, suy ra:
Vậy bán kính đáy là a√2/2.
3.2. Tìm Diện Tích Đáy
Ta sử dụng công thức diện tích hình tròn: πr².
Ví dụ: Khối trụ có diện tích toàn phần gấp đôi diện tích xung quanh, bán kính đáy 6cm. Tính thể tích.
Giải: Diện tích toàn phần gấp đôi diện tích xung quanh, nên 2πrh + 2πr² = 2(2πrh) => h = r = 6cm. Vậy V = π.6².6 ≈ 678.6 cm³.
3.3. Tìm Chiều Cao
Có thể sử dụng định lý Pytago nếu đề bài cho độ dài đường chéo.
Ví dụ: Khối trụ có thể tích 12π, chu vi đáy 2π. Tính chiều cao.
Giải: Bán kính r = 2π/(2π) = 1. Chiều cao h = V/(πr²) = 12π/π = 12.
viết bài văn phân tích một tác phẩm văn học bài thơ thất ngôn bát cú hoặc tứ tuyệt đường luật
4. Bài Tập Vận Dụng
Dưới đây là một số bài tập vận dụng kèm lời giải:
Một số bài tập tính thể tích khối trụ tròn xoay
(Bài 1, 2, 3 – Giữ nguyên nội dung lời giải của bài viết gốc)
Kết Luận
Bài viết đã trình bày tổng quan về khối trụ tròn xoay, công thức tính thể tích và các dạng bài tập thường gặp. Hy vọng bài viết này hữu ích cho bạn trong việc học tập và nghiên cứu về hình học không gian. Để tìm hiểu thêm về các kiến thức toán học khác, hãy truy cập website Xe Tải Sơn Tùng.